Olá pessoal, seja bem-vindo!
Neste artigo, iremos abordar um assunto que por muitas vezes passa desapercebido ou não recebe a devida importância. Hoje vamos falar sobre Amostragem! Mas, antes de começarmos, é importante definir alguns conceitos fundamentais:
População
- Conjunto de todos os elementos ou resultados sob investigação. A população pode ser finita ou infita.
Amostra
- Subconjunto de elementos da população;
- Quando tiramos algumas conclusões sobre a população estudada com base nos resultados obtidos na amostra, chamamos isso de inferência estatística.
Amostragem
Uma amostragem correta é fundamental para as pessoas que trabalham com dados. Dificilmente se consegue obter a distribuição exata de uma população. Por exemplo, imagine conseguir a idade média dos cachorros que vivem no Brasil. Podemos dizer que seria inviável e praticamente impossível por diversos fatores: cachorros não sabem falar a sua idade; pode acontecer dos donos não saberem a idade exata de seus cachorros; os cachorros em condição de rua tornaria muito díficil obter essa informação. Dessa forma, podemos coletar dados de uma amostra que seja significativa da sua população para fazer inferências a partir dessa amostra e descobrir se ela é representativa da população em questão.
Portanto, é necessário compreender os diferentes métodos de amostragem, e é isso que veremos a seguir.
Amostragem Probabilística
A amostragem probabilística é um método de seleção de amostras de uma população onde cada elemento tem uma chance conhecida e não nula de ser escolhido. Em termos simples, é como se cada item da população tivesse um “bilhete de loteria”, e a seleção fosse feita de maneira aleatória e justa, garantindo que todos os elementos tenham uma chance igual de serem escolhidos, vejamos os exemplos de amostragem probabilística:
Amostragem Aleatória Simples
Todos os N elementos da população possuem probabilidade igual de serem selecionados. Portanto, numera-se a população de 1 até N, e utilizando algum método de seleção aleatória (ex: sorteador online), escolhem-se de maneira aleatória números dessa sequência.
Exemplos:
- Sortear 5 funcionários de uma empresa;
- Sortear um livro para seus seguidores no instagram;
- Mega-sena.
Uma vantagem da amostragem aleatória simples é a fácil implementação; uma desvantagem é que casos raros podem não aparecer na seleção. Por exemplo, suponha que você tem uma loja de manutenção de celulares no centro de São Paulo e quer saber a nacionalidade das pessoas que entram na sua loja. Por estar localizada em São Paulo, a maioria das pessoas será brasileira, mas entre chineses, libaneses e colombianos, essas três nacionalidades podem ser raras na amostra.
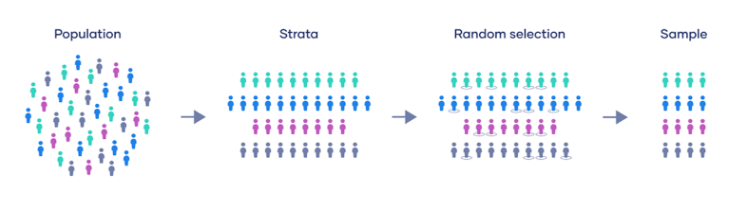
Amostragem Estratificada
Nesse método, a população é dividida em subgrupos homogêneos, chamados de estratos, com características similares entre os elementos de cada estrato. Uma vez que os estratos são criados, uma amostra é selecionada aleatoriamente de cada estrato. Isso garante que todos os subgrupos da população tenham representação na amostra final, o que pode ser especialmente útil quando há diferenças significativas entre os estratos e se deseja garantir que cada grupo seja adequadamente representado na amostra.
Por exemplo, imagine que você queira fazer uma pesquisa sobre o desempenho acadêmico em uma escola. Você pode dividir os alunos em estratos com base em suas séries escolares (por exemplo, alunos do ensino fundamental e do ensino médio) e, em seguida, selecionar aleatoriamente alunos de cada estrato para compor sua amostra. Isso ajudaria a garantir que a amostra represente de forma precisa cada grupo da escola.
Abordagem em uma amostra estratificada:
- Separar os grupos da população por estrato;
- Aplicar método de amostragem dentro de cada estrato;
- O tamanho da amostra em cada estrato pode ser proporcional à distribuição populacional dos estratos, igual em todos os estratos (uniforme), ou seguir algum critério de otimização.
Uma desvantagem desse método ocorre quando não há como dividir as amostras em grupos, principalmente quando a amostra pode pertencer a vários grupos (estratos) ao mesmo tempo.
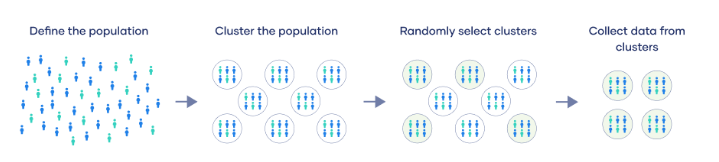
Amostra por Conglomerados
Este método é usado quando a população está agrupada em pequenos grupos (conglomerados). Ao contrário da amostragem estratificada, em que os estratos são homogêneos, na amostragem por conglomerados, os conglomerados podem ser bastante diversos internamente. Em vez de selecionar elementos individuais, como pessoas ou itens, a amostra é composta pela seleção de alguns ou todos os conglomerados da população, e, em seguida, todos os elementos dentro desses conglomerados são incluídos na amostra.
Por exemplo, ao invés de sortear alunos de uma escola da região, podemos selecionar grupos de escolas da região (conglomerados) para participar de uma pesquisa educacional.
Esse método é frequentemente mais prático e econômico, especialmente quando a população é grande e está dispersa geograficamente, já que reduz os custos de coleta de dados ao agrupar os elementos em conglomerados e selecionar alguns desses grupos para representar a população.
Uma desvantagem da amostragem por conglomerados é o aumento do erro amostral devido à heterogeneidade interna dos conglomerados.
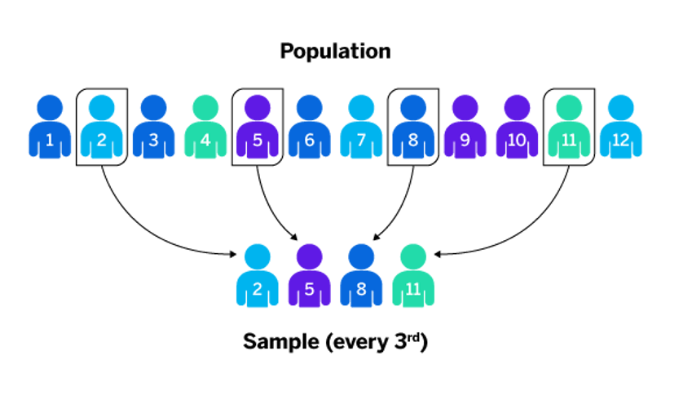
Amostragem Sistemática
Este método é utilizado para selecionar de forma sistemática e aleatória um indivíduo da população para a amostra e, posteriormente, selecionar 1 indivíduo a cada k.
Por exemplo, imagine que você trabalha em uma indústria de linha de produção de parafusos. Após uma produção diária de 1.000 parafusos, você pretende coletar 1 a cada 100 parafusos para o controle de qualidade. Portanto, ao final da coleta dos parafusos, você terá uma amostra de tamanho 10 da produção diária. É fundamental que não haja algum tipo de tendência na esteira dos parafusos.
As vantagens da amostragem sistemática podem estar na eficiência, pois é rápida de executar, e também no menor viés de seleção, caso a população esteja aleatoriamente ordenada e o padrão sistemático adotado seja apropriado.
No entanto, as desvantagens podem residir na sensibilidade aos períodos. Por exemplo, no caso da esteira de parafusos, se a esteira não estiver ordenada de forma que consigamos capturar 1 parafuso a cada 100, pode ocorrer uma variação na sistemática e levar a uma amostra não representativa.
Amostragem Não-Probabilística
Amostragem não-probabilística é um método de seleção de elementos de uma população onde cada membro não tem uma chance conhecida e igual de ser escolhido para fazer parte da amostra. Isso significa que nem todos os indivíduos da população têm a mesma oportunidade de serem selecionados.
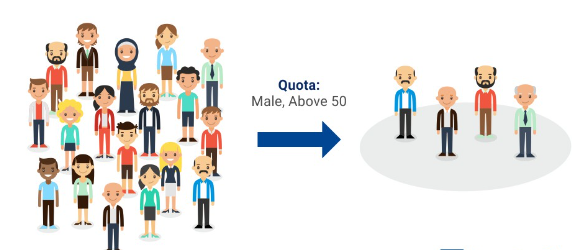
Amostragem por Cotas
Este método utilizado para garantir que certos grupos específicos da população sejam representados de maneira proporcional na amostra coletada para uma pesquisa ou estudo. Nesse método, a população é dividida em categorias ou estratos com base em características relevantes, como idade, gênero, etnia, região geográfica, entre outras.
Exemplos:
- Pesquisa de Mercado;
- Pesquisa de opinião;
- Pesquisa Eleitoral
Neste tipo de amostragem, em muitos casos pode haver viés de seleção.
Amostragem a Esmo
Neste tipo de amostragem o cientista busca ser o mais aleatório possível, mas sem fazer um sorteio formal. Por exemplo, imagine que você queira fazer um estudo sobre a água de um rio e você coleta um copo de água para avaliar sua pureza, este é um exemplo de amostragem a Esmo. Pode ser que haja algum tipo de viés? Sim, imagine coletar a água perto de um córrego de esgoto onde desagua neste rio, você concorda comigo que aquela região do rio perto do esgoto pode estar enviesando a análise da pureza do rio.
Amostragem por conveniência
Esta é uma amostra feita com voluntários ou participantes aos quais o cientista tem fácil acesso, como convidar seu grupo de amigos para participar de uma pesquisa. No entanto, este tipo de amostragem pode não generalizar muito bem, sendo bastante provável que a amostra apresente viés de seleção e não seja representativa.
Referências
MORETTIN, Pedro Alberto; BUSSAB, Wilson de Oliveira. Estatística Básica. 6. ed. Editora
Saraiva, 2010.
BOLFARINE, H e BUSSAB, WO. Elementos de amostragem. Edgar Blücher, 2005.